RDBで自己結合かつ階層が不定なツリー構造を表現するのは難しいと言われますが、不可能ではありません。
しかし、直感的でなかったり、更新時のパフォーマンス影響などがあります。
今回はRDBでツリー構造を表現するいくつかの方法とそれぞれのメリット・デメリットについて説明していきます。
隣接リスト
ツリー構造を表現するのに一番シンプルなのが、隣接リスト構造です。
隣接リストは、外部キーとして、親要素のidを持ちます。
テーブル構造としては以下のようなイメージ。

概念図
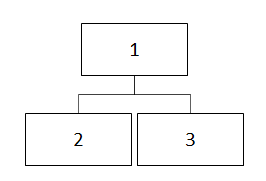
この構造のメリット、デメリットは以下です。
q
| メリット | ・構造が直感的 ・直近の親子要素を取得するのが簡単 |
|---|---|
| デメリット | ・ツリー全体を表現するのが難しい ・子を持つ要素の変更が難しい |
メリット
構造が直感的
子要素が親要素の参照を持っているというシンプルな構造であるため、直感的です。
直近の親子要素を取得するのが簡単
親要素への参照を持っているので、親要素を取得するのは簡単です。
また、子要素の取得も簡単に行えます。
自分の要素をparent_idに持っている要素をSELECTすればよいからです。
SELECT *
FROM
tree_table parent
INNER JOIN
tree_table child
ON parent.id = child.parent_id
WHERE parent.id = 123;
サブツリーの移動が簡単
ツリー内のある要素とその要素の子孫要素のまとまりをサブツリーと呼びます。
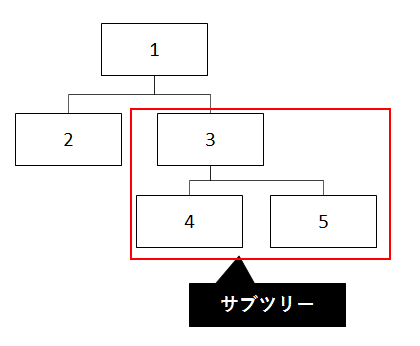
これを移動する場合、隣接リストなら簡単に行うことができます。
例えば、3を起点とするサブツリーを2の配下に移動したいとします。
その場合、3のparent_idを2に変更すればよいだけです。
UPDATE tree_table SET parent_id = 2 WHERE id = 3;
デメリット
ツリー全体を表現するのが難しい
直近の要素を取得するの簡単ですが、階層が不定になると取得が難しくなります。
例えば、先祖要素を全て取得する、子孫要素を全て取得するなどです。
階層が不定の場合、結合を何回行えばいいかわかりません。
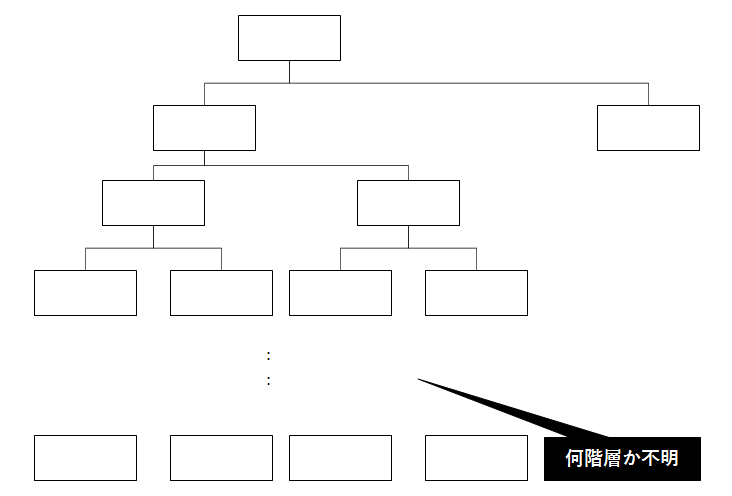
SELECT *
FROM
tree_table parent
INNER JOIN
tree_table depth1
ON parent.id = depth1.parent_id
INNER JOIN
tree_table depth2
ON depth1.id = depth2.parent_id
-- ...
-- 何回繰り返せばいい?
WHERE parent.id = 123;
ただし、階層の深さに上限が設けられているのであれば、結合の回数を定めることができます。
そう言った場合は、隣接リストを適用を検討してもいいかもしれません。
また、DBによっては、再帰的なクエリをサポートしているものもあります。
そう言ったDBMSを使用している場合は、隣接リストは最もシンプルにツリー構造を表現できる手段となります。
子を持つ要素の変更が難しい
子を持たない要素の削除や変更は比較的簡単に行えます。
挿入する場合は、親を指定すればよいだけですし、削除する場合も対象の要素の行を削除するだけです。
しかし、対象の要素が子を持っている時はもう少し複雑な操作が必要になります。
対象の要素と一緒に子要素も削除してやる必要があります。
そのためには、全ての子要素を取得する必要がありますが、これは前述のとおり、階層が不定の場合は難しくなります。
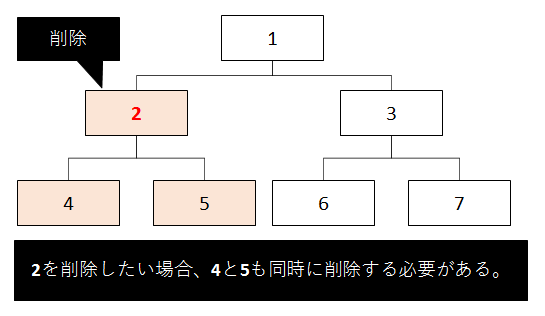
ただし、対象の要素のみを削除すれば、その配下の要素は本体のツリーとの関連がなくなります。
そのため、データとしては残りますが、ツリーの中には登場しなくなります。
ゴミデータが残ることを許容できる、定期的に一括で削除を行うのであれば、要素の削除はそれほど難しくはないかもしれません。
結論
ツリー構造をシンプルに表現することができます。
それ故にちょっとした操作を行う際にも複雑なSQLが必要になってしまいます。
ただし、階層の深さが固定であったり、ノードへの操作が挿入や更新のみである場合は、隣接リストの採用を検討してもよいです。
経路列挙モデル
その要素のpath(経路)の情報をテーブルに持たせた構造です。
例えば、以下のようなイメージになります。
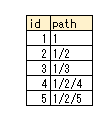
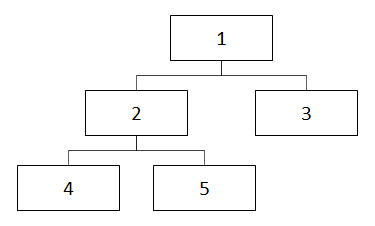
この構造のメリット、デメリットは以下です。
| メリット | ・データの操作が簡単 |
|---|---|
| デメリット | ・データの整合性を保つのが難しい |
メリット
データの操作が簡単
経路列挙モデルはデータの操作が簡単に行えます。
例えば、先祖の取得は以下のようなシンプルなクエリで実行可能です。
-- id = 2の祖先を取得する
SELECT *
FROM
table ancestor
WHERE '1/2/' LIKE ancestor.path || '%'
子孫の取得
-- id = 2の子孫を取得する
SELECT *
FROM
table child
WHERE child.path LIKE '1/2/%'
要素の削除
-- id = 2とその子孫を削除する
DELETE FROM table
WHERE path LIKE '1/2/%'
サブツリーの移動
-- id = 2とその子孫を3の配下に移動する
UPDATE table
SET path = '1/3/' || REPLACE(table.path, '1/2/', '')
WHERE path LIKE '1/2/%'
デメリット
データの整合性を保つのが難しい
pathに外部参照を設定することができません。
そのため、不正なデータが混入してしまう可能性があります。
例えば、存在しないパス、不正な区切り文字などです。
結論
要素の操作をシンプルなクエリで実現できます。
しかし、pathのフォーマットや参照整合性はアプリ側で保証する必要があります。
ツリー構造をシンプルに表現できる一方、データの整合性を保つのが難しくなります。
入れ子構造
入れ個々構造では各ノードが自分の範囲を持ちます。
仮にその範囲の始点をleft、終点をrightとしましょう。
イメージとしては以下のようなテーブル構造です。
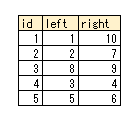
各ノードの範囲を図式化すると以下のようになります。
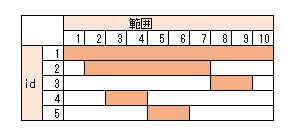
ツリーに変換するときは、自分の範囲に収まるノードを子ノートとみなします。
これをツリー構造に変換すると以下のようになります。
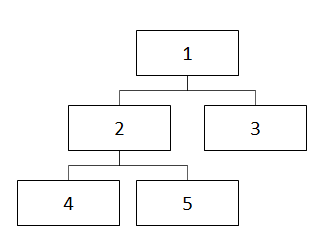
複雑な変換を要するため、直感的ではないですが、ツリー構造をシンプルなデータ構造で表現できていることがわかります。
この構造には以下のメリット・デメリットが存在します。
| メリット | ・複雑な操作が可能になる |
|---|---|
| デメリット | ・クエリの理解が難しい。 |
メリット
この構造の最大のメリットは、クエリによって柔軟な操作が可能なことです。
子孫や祖先、また直近の親子関係の取得、ツリーの階層の深さの算出など様々なことがクエリだけで実現可能です。
デメリット
デメリットは構造を理解しにくいこと、それによってクエリが複雑化することです。
またノードの挿入時に周辺ノードの左右の値を再計算する必要もあり、コストがかかります。
さらに、左右の値には制限があるため、ノードを追加できる数に制限があります。
ただし、これについては、ノード範囲のデータ型を整数でなく、実数型にすることで、解消することができます。
実数型を使用すれば、この構造の弱点は、構造やクエリの複雑さだけとなります。
結論
様々な操作をクエリだけで柔軟に行うことができます。
しかし、その分構造やクエリが複雑になり、理解が難しくなります。
閉包テーブル
閉包テーブルでは、要素と構造の情報を別々のテーブルで保持します。
イメージとしては以下のような感じです。
■要素テーブル
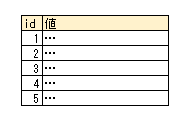
■構造テーブル
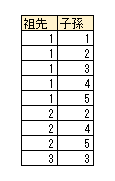
■構造イメージ図
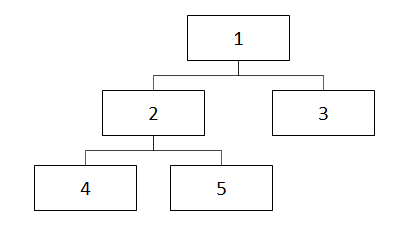
構造テーブルはその要素の子孫要素の対応を保持します。
この構造のメリットとデメリットは以下です。
| メリット | ・要素の関係を別テーブルに持っているため構造を柔軟に変更することができる |
|---|---|
| デメリット | ・直近の祖先、子孫の取得が複雑になる ・テーブルスペースが増える、更新行が多くなるなどDBのリソース消費が大きい |
メリット
閉包テーブルのメリットは、構造を別テーブルに持っているため柔軟にツリー構造を変更できる点です。
例えば新しい葉ノードは以下のように挿入することができます。
-- 新しいノードを挿入 INSERT INTO NODE (id) VALUES (6); -- 構造テーブルにデータを挿入 INSERT INTO TREE (ancestor, descendant) SELECT t.id ,6 FROM TREE t WHERE t.descendant = [挿入先親ノードのid]; -- 自己参照の行 INSERT INTO NODE VALUES (6,6);
ノードを削除するときは、そのノードを子孫に持つすべてのレコードを削除する必要があります。
具体的には以下のようなクエリになります。
-- ノードの削除 DELETE FROM NODE WHERE id = [削除するノードのid]; -- 構造を削除 DELETE FROM TREE WHERE descendant IN ( SELECT ancestor FROM TREE WHERE descendant = [削除するノードのid] );
サブツリーの移動は少し複雑になります。
まずはサブツリーのルートを構造テーブルから削除し、ツリー本体から切り離します。
-- サブツリーをツリー本体から切り離す DELETE FROM TREE WHERE descendant IN ( SELECT ancestor FROM TREE WHERE descendant = [削除するノードのid] AND ancestor <> [削除するノードのid] -- 自己参照は削除しない );
その後、サブツリーの全てのノードを挿入先親ノードとその親ノードの子孫として登録します。
INSERT INTO TREE SELECT parent.ancestor, child.descendant FROM TREE parent CROSS JOIN TREE child WHERE parant.descendant = [挿入先親ノードのid] AND child.ancestor = [サブツリーのルートid]
すこし複雑ですが、
・挿入先親ノードの祖先ノード
・サブツリーのルートノード配下の子ノード
の全ての組み合わせを挿入しています。
これにより、サブツリーの全ての要素がサブツリーより上のノードの子孫ノードとして登録されます。
このように、一部複雑な操作もありますが、SQLだけで様々な操作をおこなうことが可能です。
デメリット
直近の子孫・祖先ノードの取得が複雑
構造テーブルは、祖先と子孫の関係しか持っていません。
親と子の関係はこのテーブルから直接知ることはできません。
入れ子構造の時と同じような操作をしないといけません。
・祖先ノードを全て取得
・祖先ノードごとに基準ノードまでの間に存在するノードを取得
・間のノードが存在しないものが直近の親となる
SELECT t1.oya FROM TREE t1 -- ②①と①が保持する子の組み合わせを生成 -- ただし、自己参照の行と対象ノード(3)は除く -- また、対象ノードが子として保持しているものも組み合わせから除外する -- これにより、そのノードの子孫かつ対象ノードの子孫ではないものが抽出される LEFT OUTER JOIN TREE t2 ON t1.oya = t2.oya AND t2.ko <> 3 AND t2.oya <> t2.ko -- 対象ノード(3)が子として保持しているものを除外 AND t2.ko NOT IN ( select t3.ko from TREE t3 where t3.oya = 3) -- ①3を子に持つ要素を抽出 -- 自己参照は除外 WHERE t1.ko = 3 AND t1.oya <> 3 -- ③②が0件=直近の祖先(親)である GROUP BY t1.oya HAVING COUNT(t2.oya) <= 0;
このように複雑な操作を行わないといけなくなります。
しかし、構造テーブルにツリーの深さを項目として持てば、もっとシンプルなクエリで取得することができます。
対象ノードの深さ±1である祖先(子孫)を取得することで直近の要素を取得できます。
ただし、その際は要素の異動や削除の際に深さを更新する必要があります。
場合によっては大量のレコードを更新する可能性もあります。
DBのリソースを消費する
要素と構造を別テーブルに分けるため、単純にテーブルのスペースを消費してしまいます。
また親ノードとすべての子孫ノードの対応を持つため、ツリーの階層が深くなればなるほど、レコードの数は急速に増えていきます。
100階層のツリーに101階層目のノードを追加すると、101レコードに変更が必要になります。
これがサブツリーの異動になると更新量はさらに増えます。
まとめ
ツリー構造をRDBで表す方法は複数の種類があります。
RDBでツリー構造を表現するのは難しいため、どう表現しても欠点があります。
そのため、複数の方法が存在するのです。
それぞれの表現方法のメリット・デメリットを考慮し、システムの要件にあった構造を選択することが重要になります。