DB設計において避けては通れない正規化について解説していきます。
正規化について
正規化とは、外部スキーマで定義したデータをDB上で効率的に管理するために整理、分割をする作業のことを指します。
この正規化には、第一正規化~第五正規化とボイスコッド正規化が存在します。
ただし、一般的に使われるのは、第一正規化~第三正規化までのことが多いです。
では、第一正規化から順番に見ていきます。
第一正規化
第一正規化は、一つのカラムに一つの値のみを持っている状態にすることを指します。
例えば、以下のようなテーブルが存在するとしましょう。
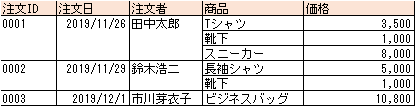
このテーブルは、注文に対して複数の商品が紐づいています。
これは概念的には間違っているようには見えません。
実際に注文には複数の商品が紐づくことがあります。
この構造の問題は、それをデータベースで表現することができない点です。
データベースでは、一つの値を配列にしたり、入れ子構造にしたりすることができません。
もし、データベースでこうした構造を表現したいなら、以下のようにする必要があります。
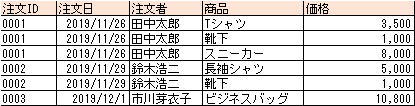
この状態は、一つのカラムに一つの値のみが入っている状態になります。
これが、第一正規化が完了した状態となります。
第二正規化
第二正規化は、部分関数従属を排除したもののことです。
部分従属とは、複合主キーの一部によって定まる値のことを指します。
例えば以下のようなテーブルは、部分関数従属していると言えます。
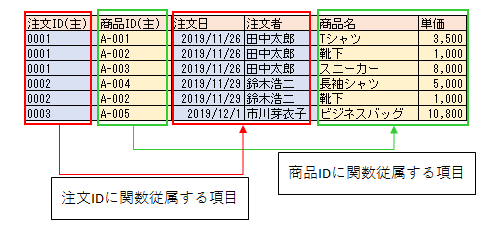
それぞれの項目が、主キーの一部である「注文ID」、「商品ID」のいずれかに関数従属しています。
注文日や注文者は注文IDによって定まり、商品名や商品単価は商品IDによって定まります。
では、なぜ部分関数従属しているといけないのでしょうか。
これは、部分関数従属している値を変更するときのことを考えてみるといいです。
例えば、商品ID「A-001」の「Tシャツ」の名称を変更するとします。
そうした場合、「A-001」を参照する注文すべてに対して更新をかけないといけなくなります。
これは非効率ですし、更新中に参照された場合、一方は新名称でもう一方は旧名称になっているなどの不整合も発生します。
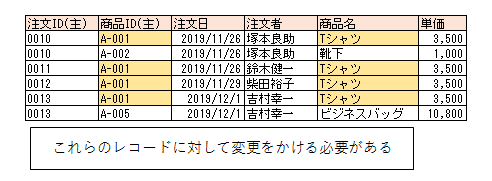
第二正規化をすることによって、そうした無駄が排除されます。
部分関数従属を排除し、第二正規化された状態のテーブルが以下になります。
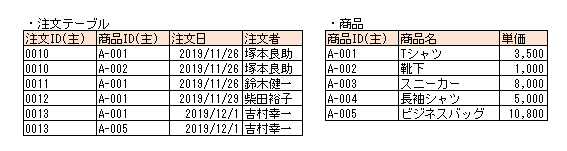
部分関数従属を排除するにはこのように部分関数従属する属性を別テーブルとして切り出してやればいいです。
こうすることで、商品名を変更したいとなった場合も、該当の商品レコードを1行更新してやれば済みます。
しかし、この状態でもまだ完全に部分関数従属を排除できていません。
以下の図のように、注文日や注文者は複合主キーの一部である注文IDにのみ依存しています。
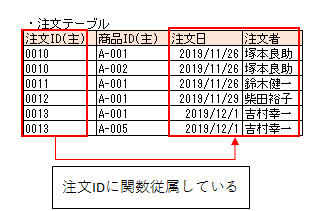
この部分関数従属を切り離すために、注文IDと商品IDの関連付けだけを現した別テーブルを切り出します。
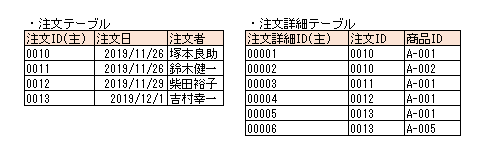
こうすることにより、全ての項目が主キーに完全関数従属する状態となりました。
第三正規化
第三正規化とは、推移的関数従属を排除した形式のデータになります。
推移的関数従属と言うのは、二段階以上で関数従属しているような項目のことを指します。
例えば、以下のようなテーブルは推移的関数従属しているということができます。
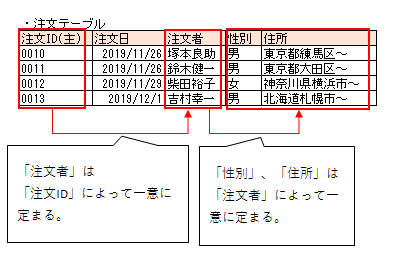
「注文者」は「注文ID」に関数従属しています。
そして、「性別」や「住所」は「注文者」に関数従属しています。
つまり、「注文ID → 注文者 → 性別、住所」というように連鎖的に関数従属していることがわかります。
この時、「性別」や「住所」は「注文ID」に推移的関数従属しているということができます。
推移的関数従属を排除すると以下のようなテーブル構造になります。
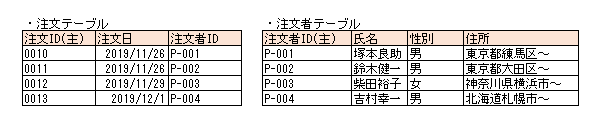
ボイスコッド正規化
通常の業務であれば、第三正規形まで完了させればデータとしては問題ないことが多いです。
しかし、業務においては、第三正規形よりも高次の正規化を求められることがあります。
そこで、第三正規形以降の正規化についても解説していきます。
第三正規化の次にあるのが、ボイスコッド正規化と呼ばれるものです。
第3.5正規形と呼ばれることもあります。
ボイスコッド正規形は、キーから主キーへの関数従属を排除したものになります。
例えば、以下のようなテーブルは第三正規形を満たしていますが、ボイスコッド正規形を満たしてはいません。
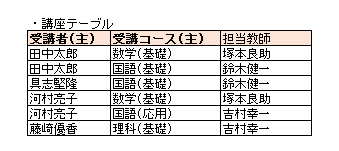
このテーブルは、「受講者」と「受講コース」が主キーとなっています。
「担当教師」はそれぞれ教えることができる「受講コース」が決まっています。
また、「受講コース」を教えることができる教師は一人だけという前提にします。
この時、「担当教師 → 受講コース」の関数従属が発生しています。
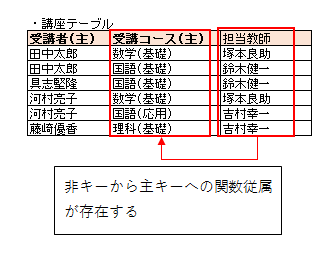
これは、非キーから主キーへの関数従属となります。
つまり、ボイスコッド正規形の条件を満たしていないということになるのです。
この問題点としては、受講されないとそのコースをテーブルに登録できないという点です。
(むしろ受講者がコースを選択する際は、先にコースが存在していないとだめですよね。)
これを解消するためには、「受講コース」と「担当教師」の関連を別テーブルに切り出してやる必要があります。
以下がボイスコッド正規化を満たしたテーブル構造になります。

(しかし、「受講コース」が「担当教師」によって定まるこのテーブル構造には違和感があります。
また、「受講コース」に対してそれを開講可能な教師が常に一人と言うのもおかしな話です。
現にこのテーブル構造だと、一つの講座を複数の教師が開講可能となった場合、元のテーブルに戻せなくなります。
そう考えると、通常の業務でボイスコッド正規形を満たさないテーブルと言うのは、なかなか作られないものなのかもしれません。)
また、以下のように「担当教師」を主キーとすることでもボイスコッド正規形とすることができます。
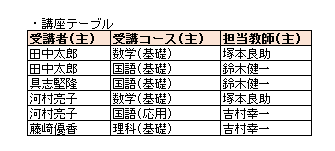
しかし、これは第四正規形の条件であるテーブル内に複数の多値従属性を持たないようにするの原則を破っています。
これについては、第四正規形の項で詳しく説明していきます。
この手の話は、いろいろな具体例を見ていく事が理解の近道となります。
以下のページを読んでみることで、さらに理解が深まると思います。
「特殊な正規形」を理解する (1/2)
ボイスコッド正規化 - Qiita
第四正規形
第四正規形は、複数の多値従属を排除することで実現できます。
多値従属性とは、ある項目によってある項目群が定まることを指します。
例えば、以下のテーブルを見てみましょう。
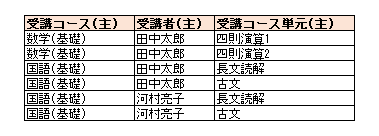
このテーブルは以下のような業務ルールに従って作成されています。
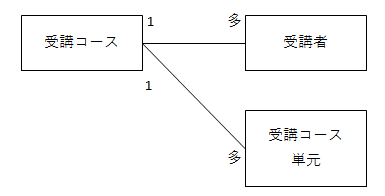
「受講コース」は複数の「受講者」に紐づく可能性があります。
また「受講コース」と「担当教師」は1対1の関係にあります。
受講者は単元を単体で受講することはできず、コース内でセットになっているものを全て受ける必要があります。
このテーブルでは、「受講コース」によって「受験者」群が定まります。
群と言っているのは、一つのコースが複数の受験者に関連する可能性があるためです。
また、「受講コース」によって「受講コース単元」群も定まります。
ここで群と言っているのも、上記と同じ理由です。
つまり、このテーブルには以下のような二つの多値従属性が存在することになります。
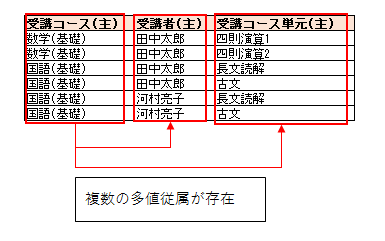
複数の多値従属が存在すると、レコード更新時に不整合が発生しやすくなります。
例えば、コースの担当教師が変わった時に、該当のレコードを全て更新しないといけません。
また、「受講コース」と「担当教師」の整合性が保障されません。
本来はそのコースを担当していない教師でも、担当教師として登録することができてしまいます。
このテーブルから複数の多値従属性を排除すると以下のようなテーブル形式になります。
それぞれの多値従属を別のテーブルに切り出した形になりますね。

これは、ボイスコッド正規形の項でみたものと同じ切り分けになります。
業務ルールとして、受講者は単元を個別で受講することはできないので、結合によって元の表に戻すことも可能です。
第五正規形
上記で第四正規形が完了しました。
ここで、業務ルールに変更を加えてみます。
「受講者」は単元を個別で受講することができるようになります。
このルールが適用されると、分割後の表は元の表に復元することができなくなります。
例えば、以下の表のように、田中太郎は「四則演算1」の単元のみを受講しているとします。

この時、分解後の表では、復元ができません。
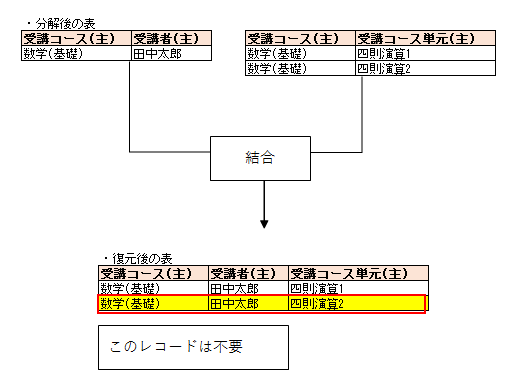
この表には、部分関数従属、推移的関数従属、複数の多値従属のどれも存在していません。
では、なぜこの分割で上手くいかないのでしょうか。
実は、この元の表はこの時点で第四正規形を満たしています。
「受講コース」によって「受講者」群は定まりますが、「受講コース単元」群は定まりません。
なぜなら、「受講コース単元」は「受講者」ごとに異なるためです。
(※「受講者は個別に単元を受講できる」という業務ルールに変更になったため。)
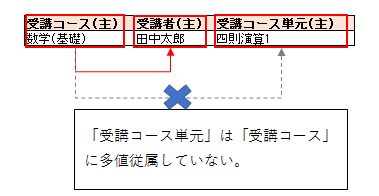
これはつまり、受講者と受講コース単元の間に関連性が生まれたことが原因となります。
今までと業務ルールが以下のように変更になったことを意味します。
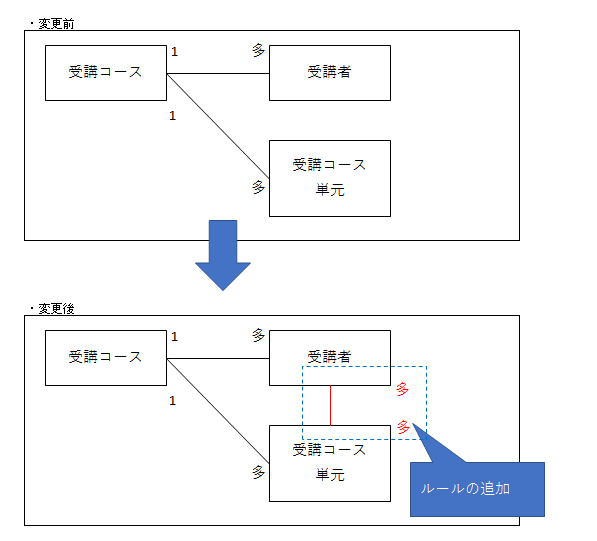
この図からわかるように、このデータ形式だと新たに追加された「受講者」と「単元」の関係性が表現されていないのです。
そのため、元の表に戻すことができなくなっているのです。
新たに追加された関係を表現したテーブル構造は以下になります。
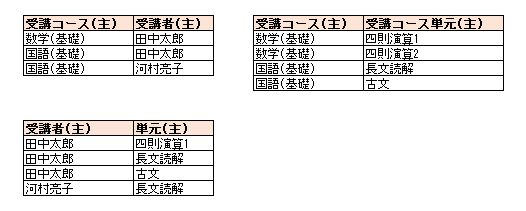
第五正規形は、第四正規形を満たしているが元の表に復元できない場合、表現しきれていないリレーションを表現する作業ということができます。